How to solve indefinite integral of 2x plus 3 rise to 9 by dx ?
Short answer: indefinite integral of 2x plus 3 rise to 9 by dx is (((2x+3)^10)/20)+C. ∫ ((2x+3)^9)dx is not particulary hard integral. You can solve it in 9 easy steps. We will walk you through and explain everything. Let's start.
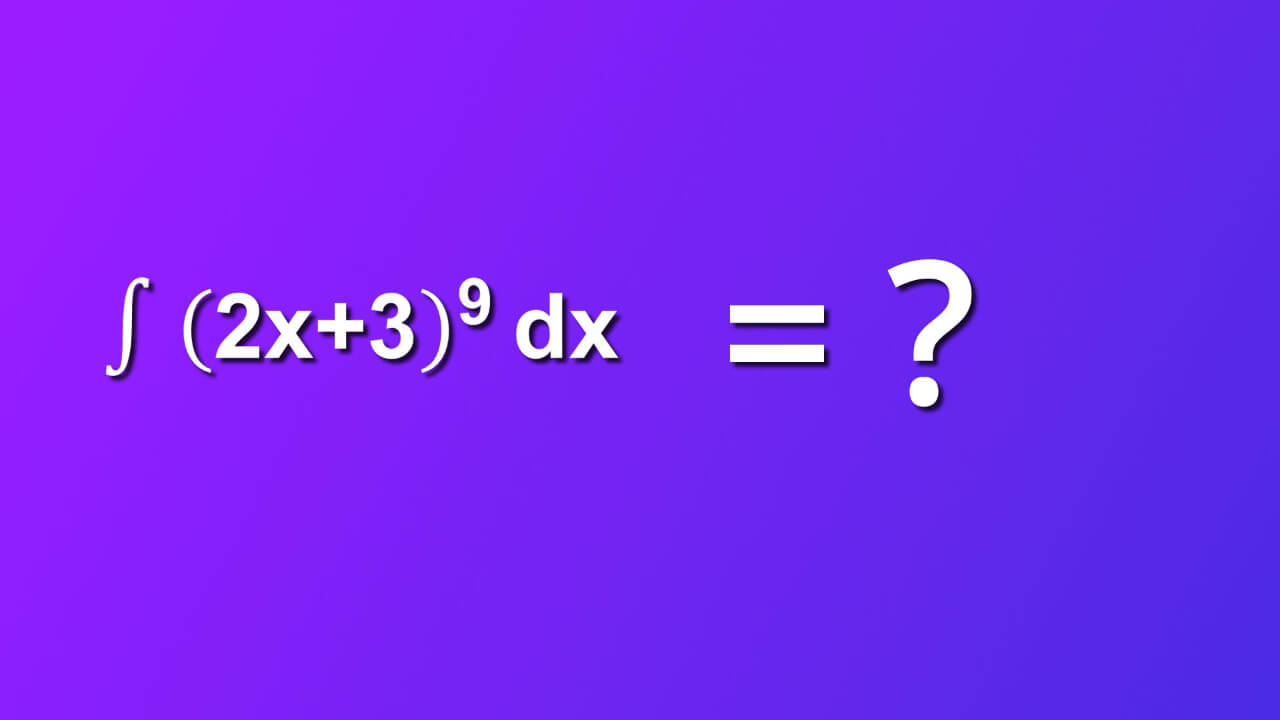
Table of contents
- Required assumtions
- Step by step solution of ∫ ((2x+3)^9)dx
- What is indefinite integral of 2x plus 3 rise to 9 by dx?
- Full video how to solve ∫ ((2x+3)^9)dx
- Dictionary
- Want to solve next one?
Required assumtions
Usually, we have some additional info about function f of (x). In our case:
- f(x) belongs to real numbers
- f(x) is integrable in that domain
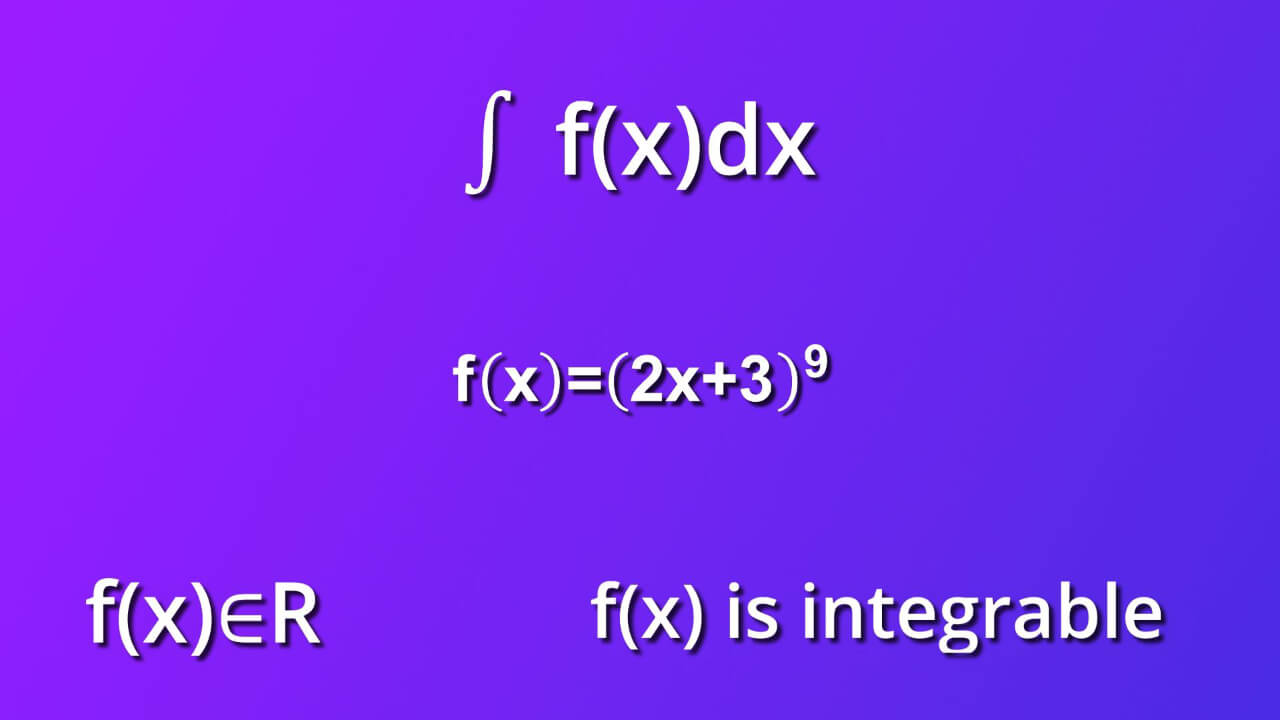
Step by step solution of ∫ ((2x+3)^9)dx
We will solve ∫ ((2x+3)^9)dx in 9 easy steps. Let's get started
Step 1
From symbol dx we know that differential of variable x indicates that the variable of integration is x. In that case, to solve this integral we may apply so called u−substitution method. We do it in order to modify the integral in the way that enable using some of formulas for finding integrals. In our case we substitute expression 2x plus 3.

Step 2
We say u is equal to 2x plus 3. We also have to know what is the derivative of u. So we write derivative of u equals to d 2x plus 3. From rules that we can apply to derivatives, we know that derivative of 2x plus 3 equals derivative of 2x plus derivative of 3. Thus, we have du equals d 2x plus d3. We also know that derivative of constant is 0. Consequently, our derivative of 3 is also 0. And we’ve got du is equal to 2 dx. But what we want to have is expression that we insert to our main solution instead of dx. So, after division of both sides by 2 we’ve got du divided by 2 is equal to dx that we were searching for now.
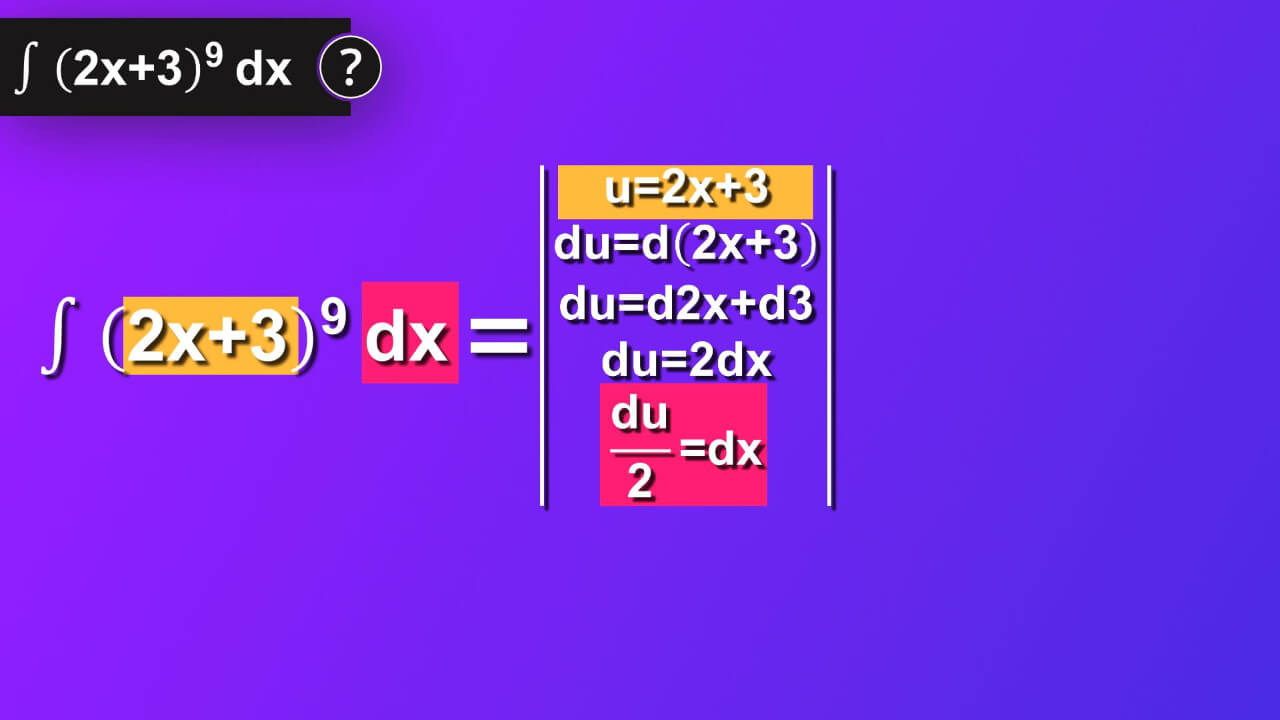
Step 3
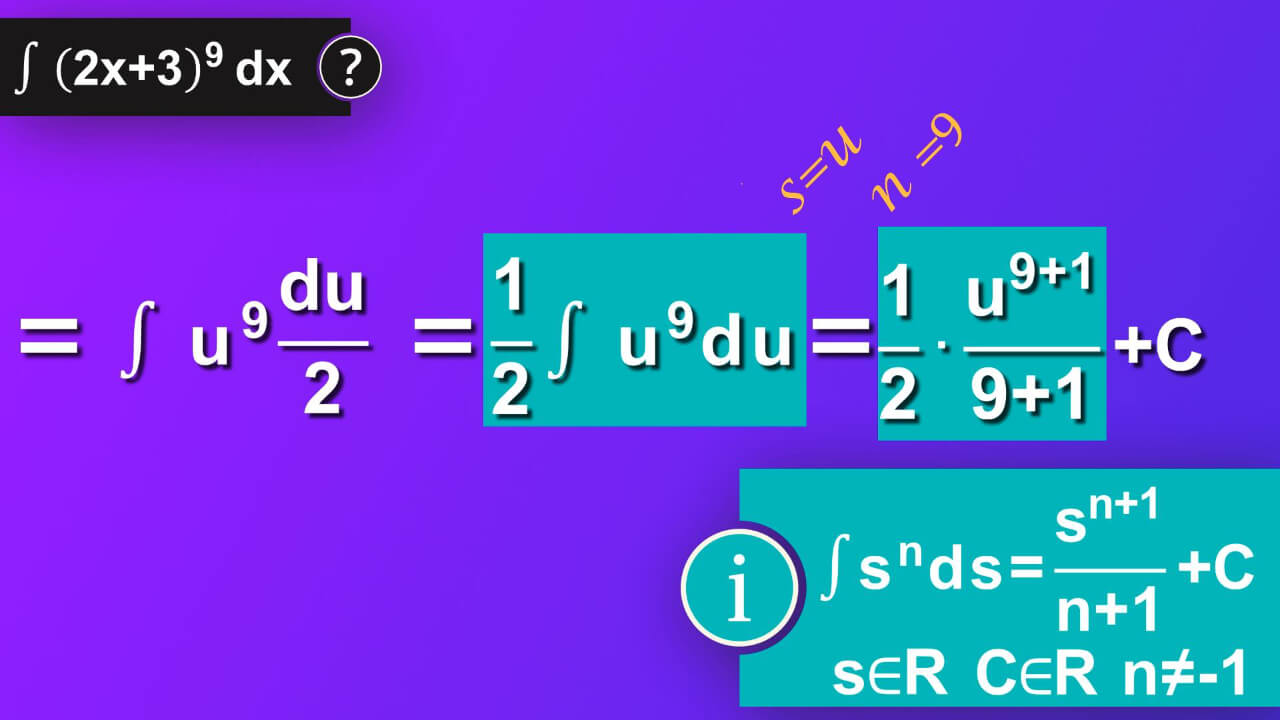
Let’s make use of our u. We insert u instead of 2x plus 3 to our main equation and instead of dx we now use expression with our substituted variable u which is du divided by 2. We have now integral of u rise to 9 by du divided by 2.
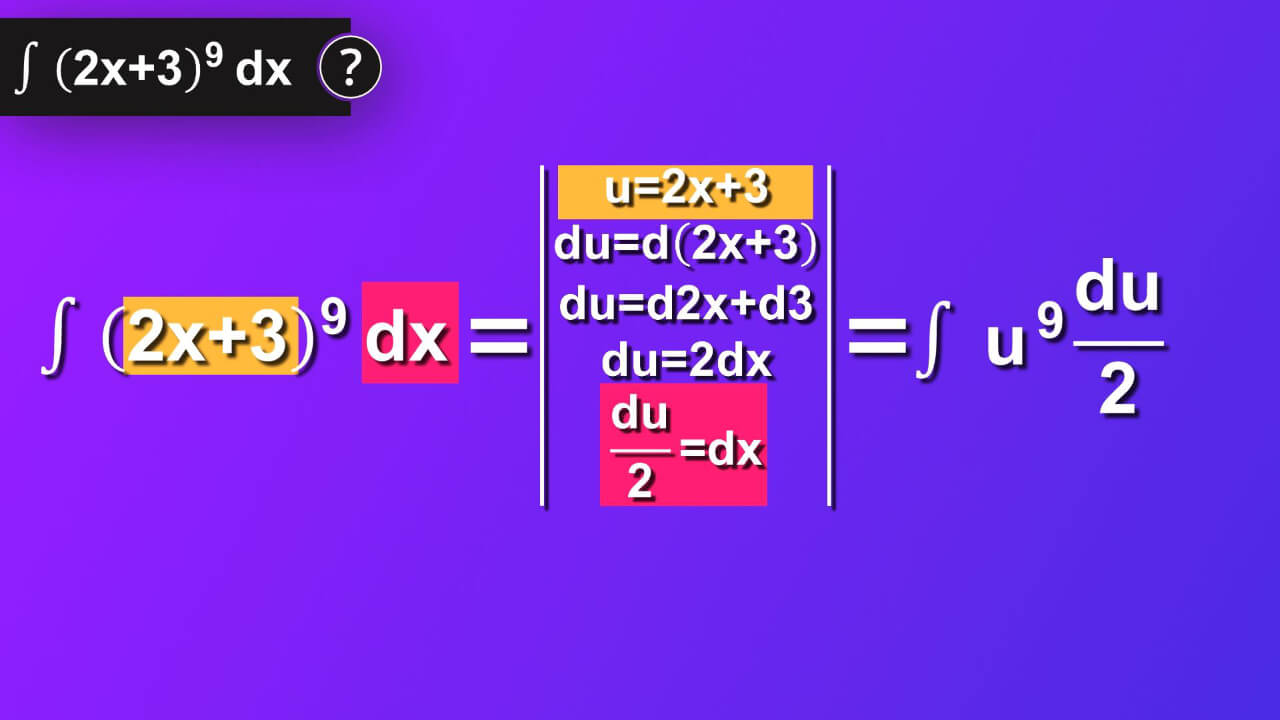
Step 4
Next, we try to modify our main equation to the form which enables using some known formula for solving integral. First, knowing that integral of a multiplied by s by ds, where a is some constant equals a multiplied by integral of s by ds, we may apply it to our equation. In our case s is u rise to 9 and a is a half.

Step 5
Perfect, now we can apply formula for solving integral of s rise to n which is s rise to n plus 1 divided by n+1. We also must add constant C to make sure that we have all our solution taken into account as our solution make whole class of function not a single one. In our case s is equal to u and n is 9.

Step 6
We’ve got a half multiplied by u rise to 9 plus 1 divided by 9 plus one and plus constant C.
Step 7
Thus, we may write it as a half multiplied by u rise to 10 divided by 10 and going further, when we multiply a half by u rise to 10 divided by 10,

Step 8
we will get in numerator u rise to 10 and in denominator 20 plus constant C.

Step 9
But it is not the end of our solution. We have to come back to our problem, and it was formulated using variable x. We’ve used u-substitution and now we have to come back to x. So instead of u we now insert 2x plus 3. We’ve got 2x plus 3 rise to 10 and divided by 20 plus constant C as a result of our problem.
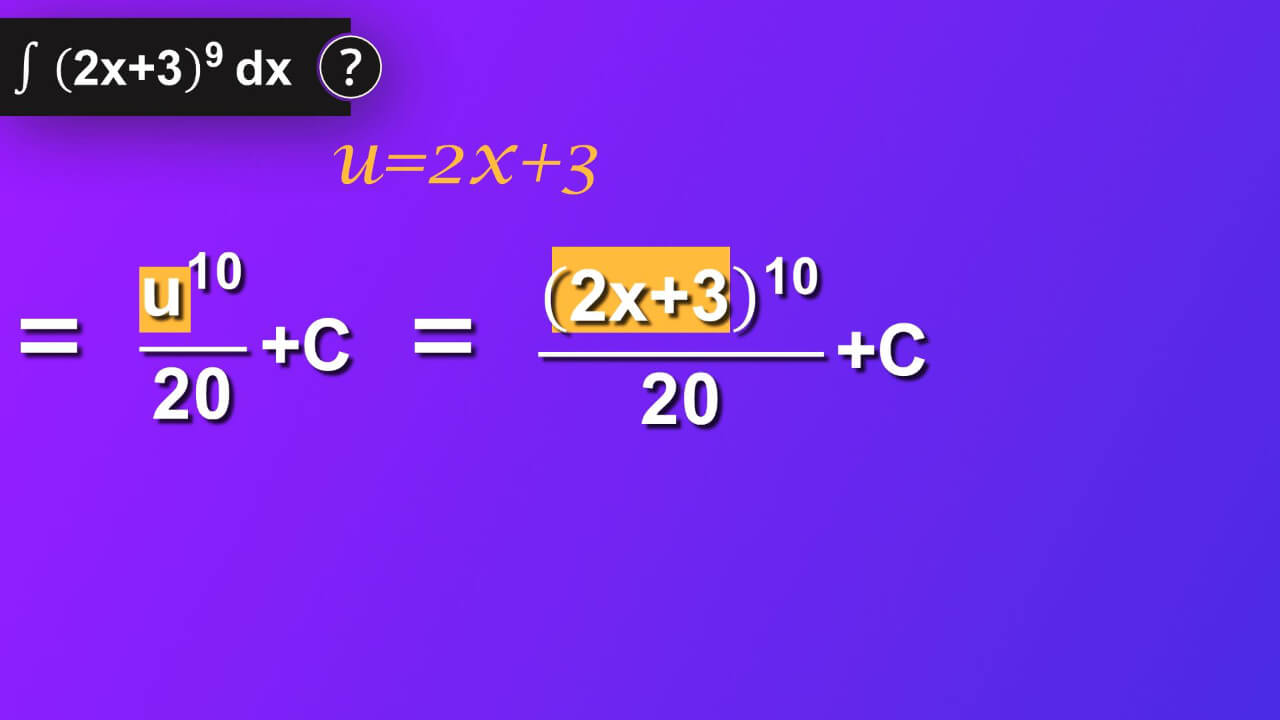
What is indefinite integral of 2x plus 3 rise to 9 by dx?
We finally did it: ∫ ((2x+3)^9)dx=(((2x+3)^10)/20)+C
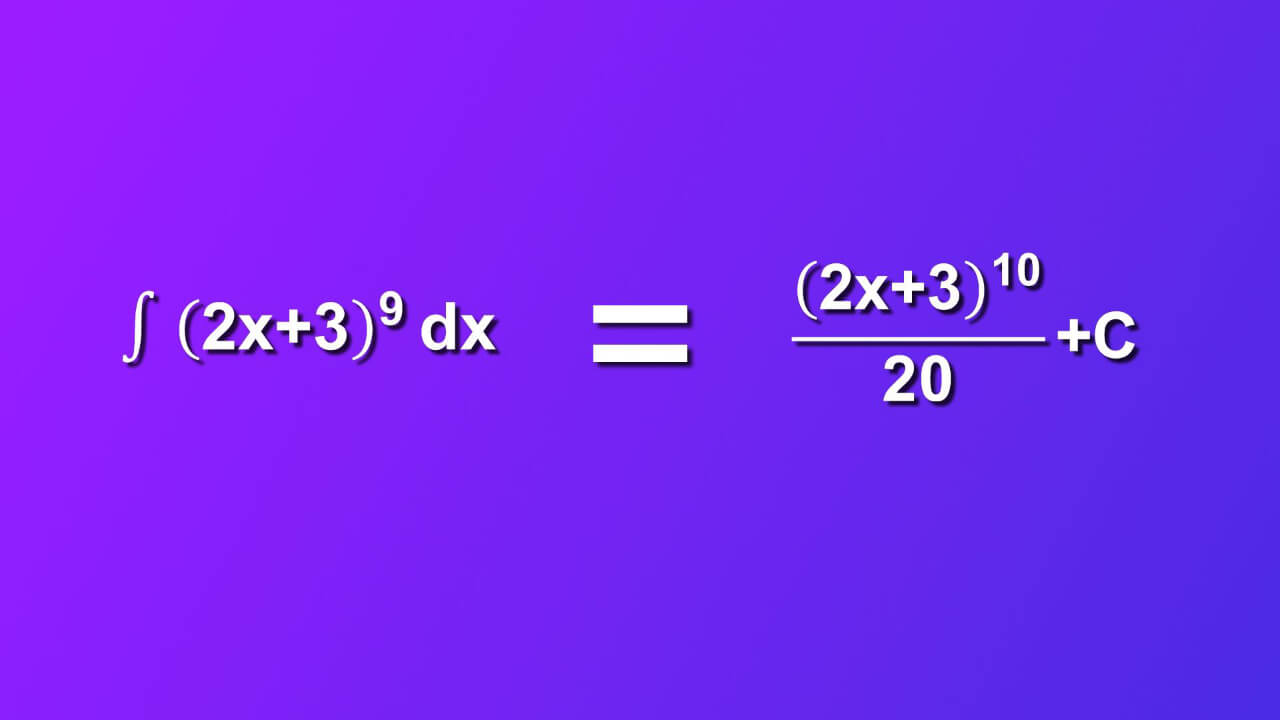
Dictionary
Integration (antidifferentiation)
Computation (process of finding) of an integral, opposite process to differentiation.Integrand
Function placed between sign of integral and differential of variable of integration e.g. $${{ \int f(x)dx}}$$,where:
$${{ \int }}$$- integration operator,
f(x) – integrand,
dx- differential of variable of integration x
Integrable function
Function that integral over its domain is finite.Indefinite integral
Represents a class of primitive functions whose derivative is the integrand e.g. $${{\int f(x)dx=F(x)+C \Leftrightarrow F’(x)=f(x)}}$$$${{C=const. }}$$,
$${{f, F,C \in R }}$$
R-real numbers
$${{\int f(x)dx}}$$ - indefinite integral of function f(x) by dx,
$${{F(x)+C}}$$ – a class of primitive functions that $${{F’(x)=f(x) }}$$,
F(x) - primitive function, usually written in capital letters,
R-real numbers.
Integration by substitution, substitution method, u-substitution
Method used to solve integral when an integral contains some function and its derivative. The function we sat as equal to u and we rewrite the integral using a new variable u.$${{\varphi: x \rightarrow \varphi (x)=u, x \in X, u \in U}}$$
and
$${{f: u \rightarrow f(u), u \in U, f(u) \in \varphi }}$$
$${{\varphi}}$$ is injective and differentiable function in X
f is continuous in U
then, $${{ \int f(\varphi (x)) \varphi’(x)dx=f(u) du}}$$ $${{\int f(\varphi (x))\varphi’(x)dx=\Bigg|\matrix{u= \varphi (x) \cr d(u)= d(\varphi (x))\cr du= \varphi ’(x) dx}\Bigg| =\int f(u) du}}$$
Function
Function specified on a set X and having values in set Y is an assignment each element of set X specifically one element in set Y.$${{f: X \rightarrow Y}}$$
f-function name,
X-set of elements of function f, domain of a function f
Y-set of function values of function f, codomain of a function f
$${{x\in X, y \in Y}}$$
$${{y=f(x) f: x\rightarrow y}}$$
$${{y=y(x), }}$$
y(x)-vales of the function named y,
x-independent variable,
y-dependent variable.
Derivative, derivative of a function
If $${{lim {\Delta f \over \Delta x }}}$$exists (and is finite), then this limit is named$${{ \Delta x\rightarrow 0}}$$
derivative of a function f(x) in a point x0 and use symbol f’(x).
$${{ f’(x_0) {\buildrel\rm def\over=} \lim_{\Delta x\to0} {\Delta f \over \Delta x}}}$$
Derivative function f’(x)
Derivative function of function f(x) is a function that values in a point x_0 are equal to derivative of this function in the point x_0.f’(x_0) - derivative of a function f(x) in a point x_0 (a number, because it is a specifically determined limit of a function),
f’(x)-derivative function.
Differentiable function
f(x) is differentiable in a point x_0 means that there exists f’(x_0 )-f(x) is differentiable in (a,b) means there exists f’(x), x $${{\in(a,b) }}$$
-f(x) is differentiable in



