How to solve indefinite integral of cosine 5x by dx ?
Short answer: indefinite integral of cosine 5x by dx is (1/5)(sin5x)+C. ∫ (cos5x)dx is not particulary hard integral. You can solve it in 7 easy steps. We will walk you through and explain everything. Let's start.
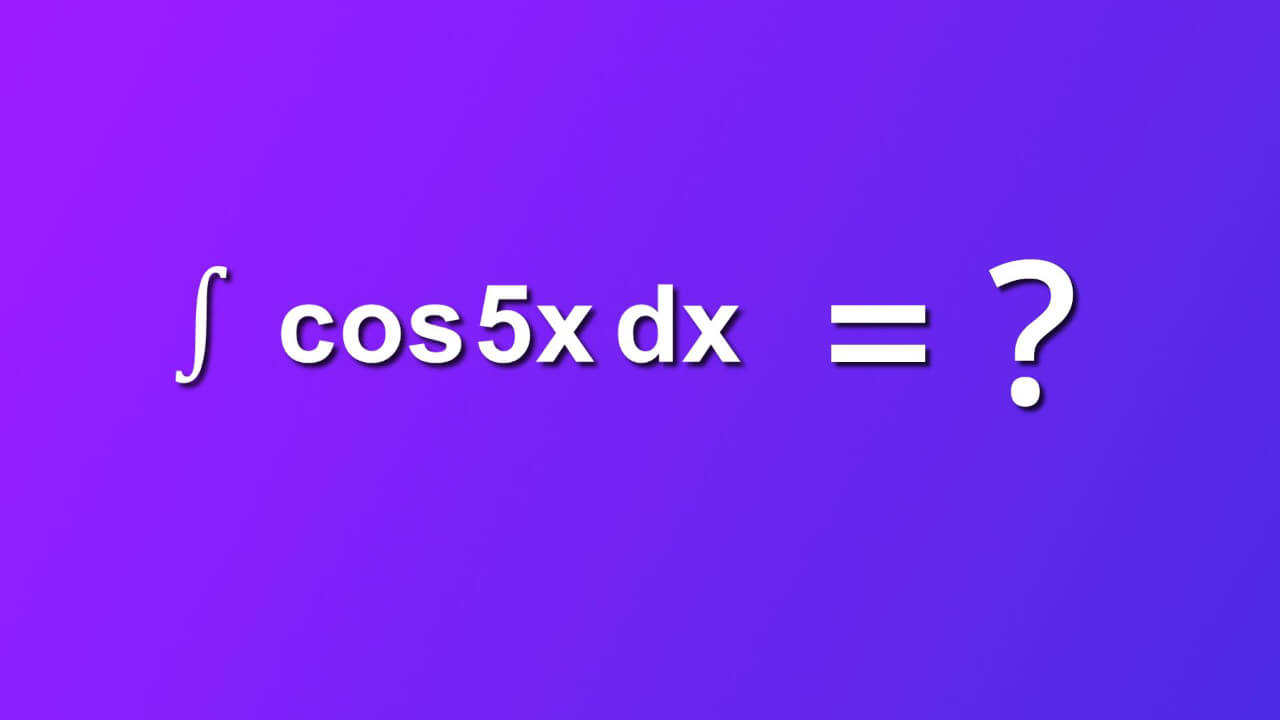
Table of contents
- Required assumtions
- Step by step solution of ∫ (cos5x)dx
- What is indefinite integral of cosine 5x by dx?
- Full video how to solve ∫ (cos5x)dx
- Dictionary
- Want to solve next one?
Required assumtions
Usually, we have some additional info about function f of (x). In our case:
- f(x) belongs to real numbers
- f(x) is integrable in that domain

Step by step solution of ∫ (cos5x)dx
We will solve ∫ (cos5x)dx in 7 easy steps. Let's get started
Step 1
From symbol dx we know that differential of variable x indicates that the variable of integration is x. In that case, to solve this integral we may apply so called u−substitution method. We do it in order to modify the integral in the way that enable using some of formulas for finding integrals. Now, we try to substitute expression 5x.

Step 2
We say u is equal to 5x. We also have to know what the derivative of u is. So we write derivative of u equals d 5x. From rules that we can apply to derivatives, we know that derivative of 5 multiplied by x is equal to 5 multiplied by derivative of x. Thus, we have du equals 5 multiplied by derivative of x. But what we want to have is expression that we insert to our main solution instead of dx. So, after division of both sides by 5 we’ve got du divided by 5 is equal to dx that we were searching for now. Let’s make use of our u.

Step 3
We insert u instead of 5x to our main equation and instead of dx we now use expression with our substituted variable u which is du divided by 5. We have now integral of cosine u multiplied by du divided by 5 in our main equation.

Step 4
We can rewrite this expression knowing that du divided by 5 is just one-fifth multiplied by du and as it is a constant we may put it in front of the equation and outside the integral sign. To do so we apply formula which says integral of a multiplied by s by ds, where a is some constant equals a multiplied by integral of s by ds. In our case s is cosine u and a is one-fifth.
Step 5
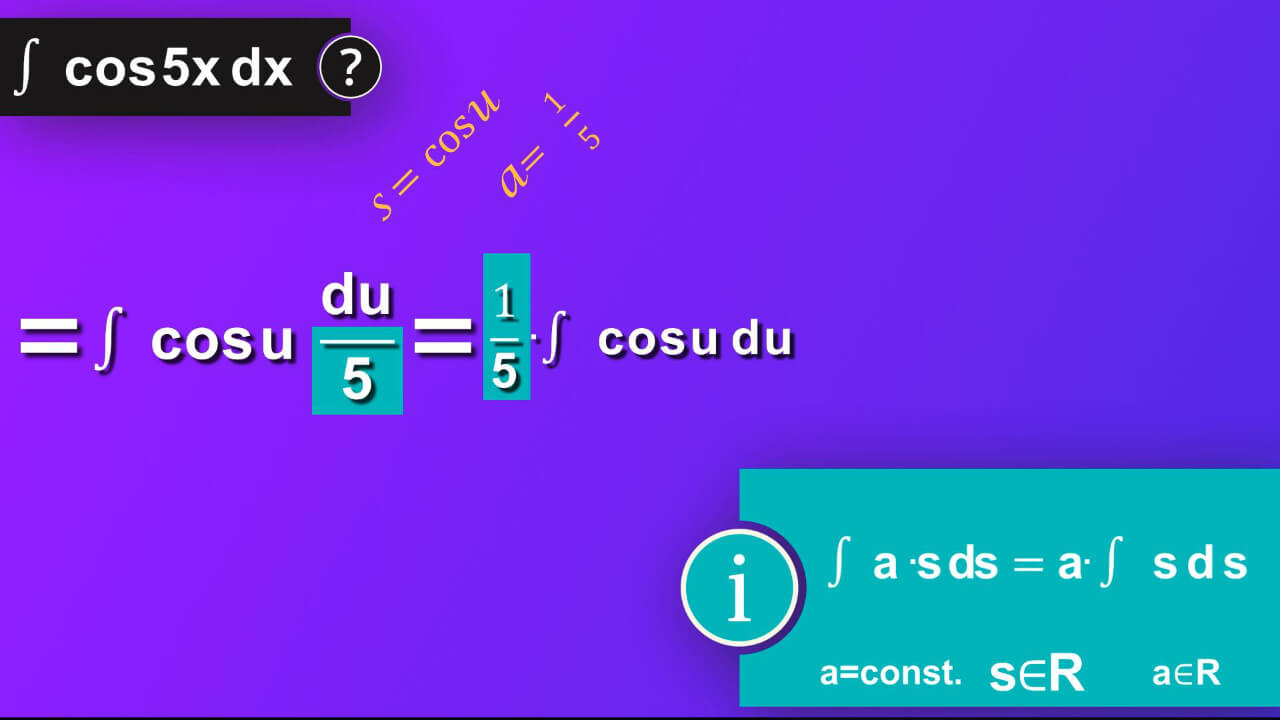
We now have our main equation as one-fifth multiplied by integral of cosine u by du. Perfect, now we can apply formula for solving integral of cosine s by ds which equals sine s. We also must add constant C to make sure that we have all our solution taken into account as our solution make whole class of function not a single one. In our case s is equal to u.
Step 6
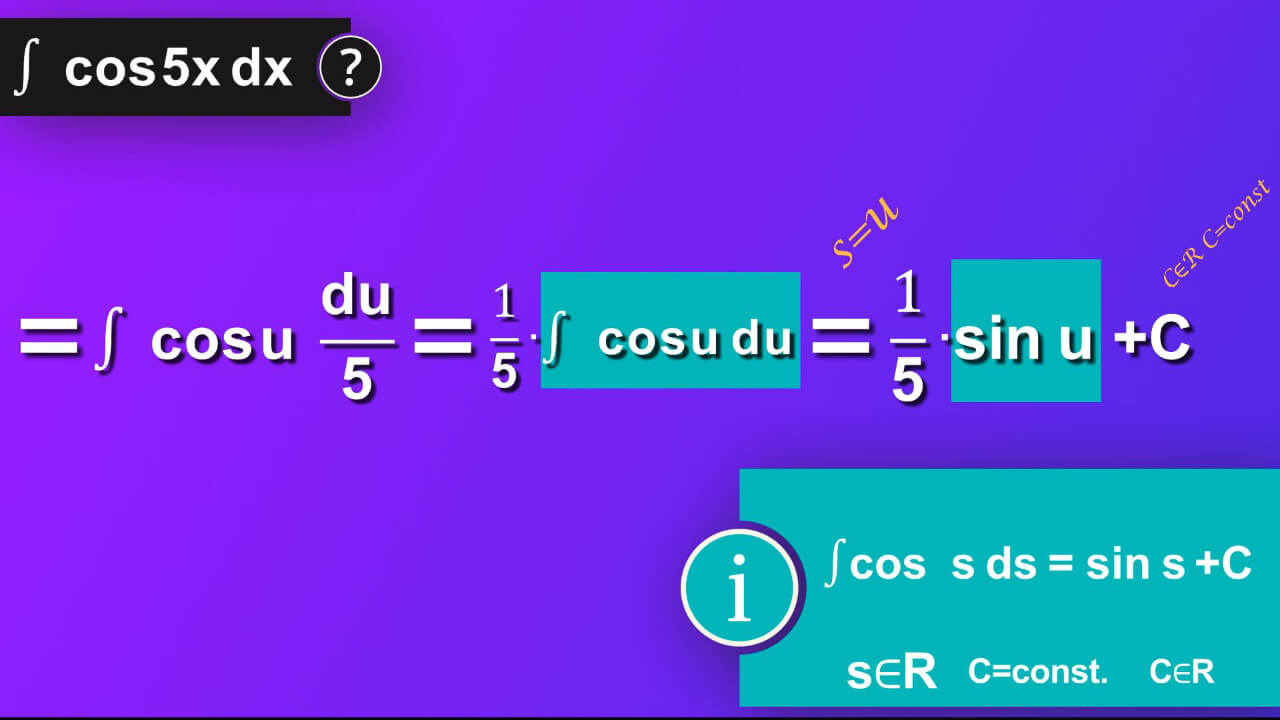
Then, we’ve got one-fifth sine u plus constant C.
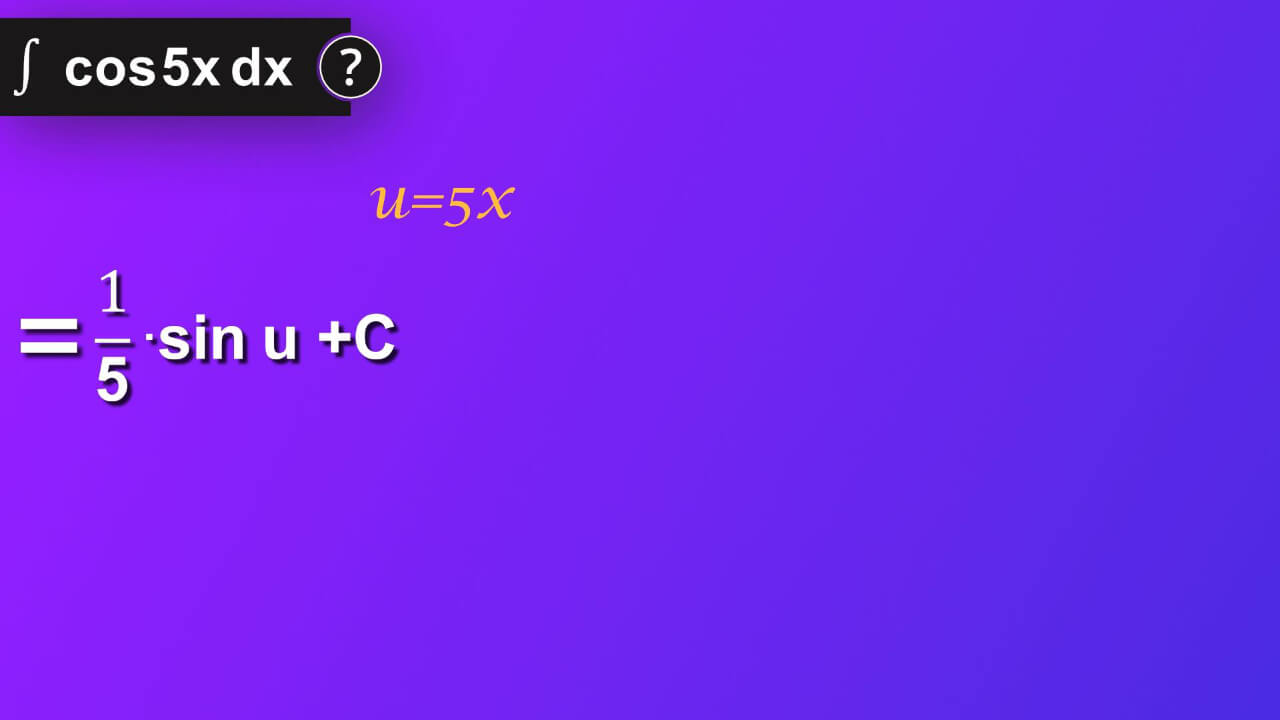
Step 7
But it is not the end of our solution. We must come back to our problem, and it was formulated using variable x. We used u-substitution and now we must come back to x. So instead of u we now insert 5x. We’ve got one-fifth sine of 5 x plus constant C as a result of our problem.
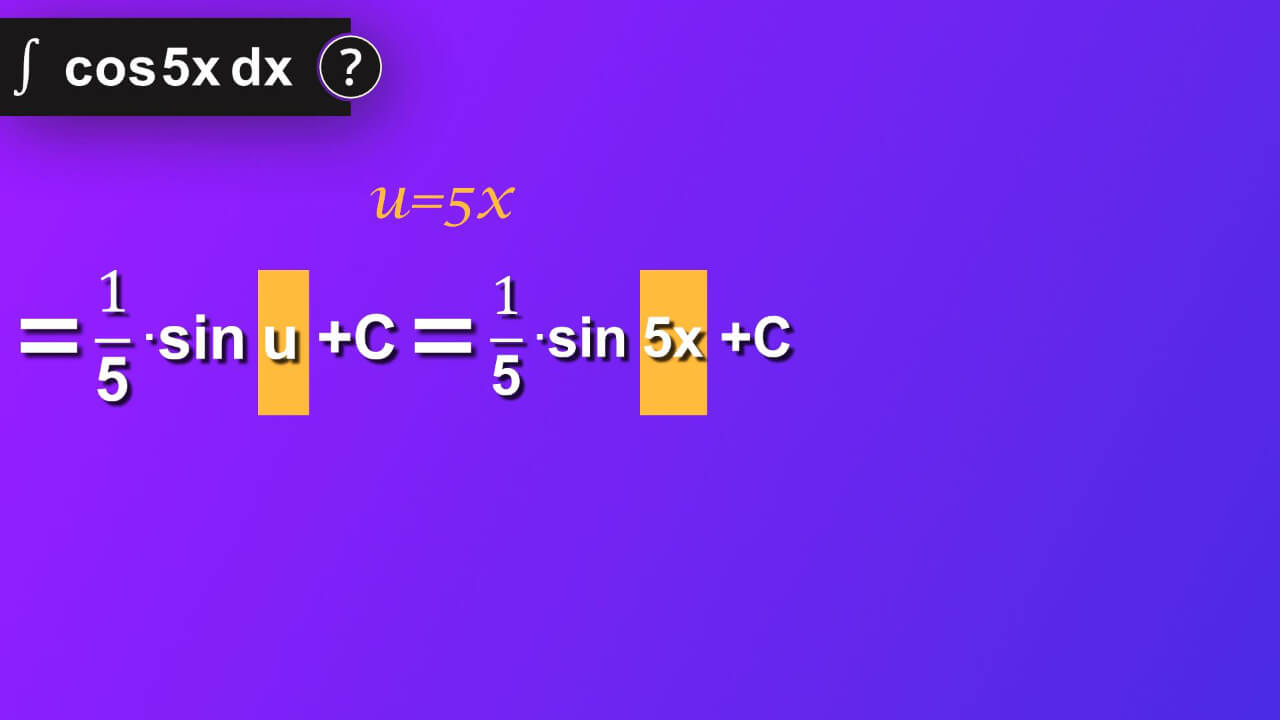
What is indefinite integral of cosine 5x by dx?
We finally did it: ∫ (cos5x)dx=(1/5)(sin5x)+C
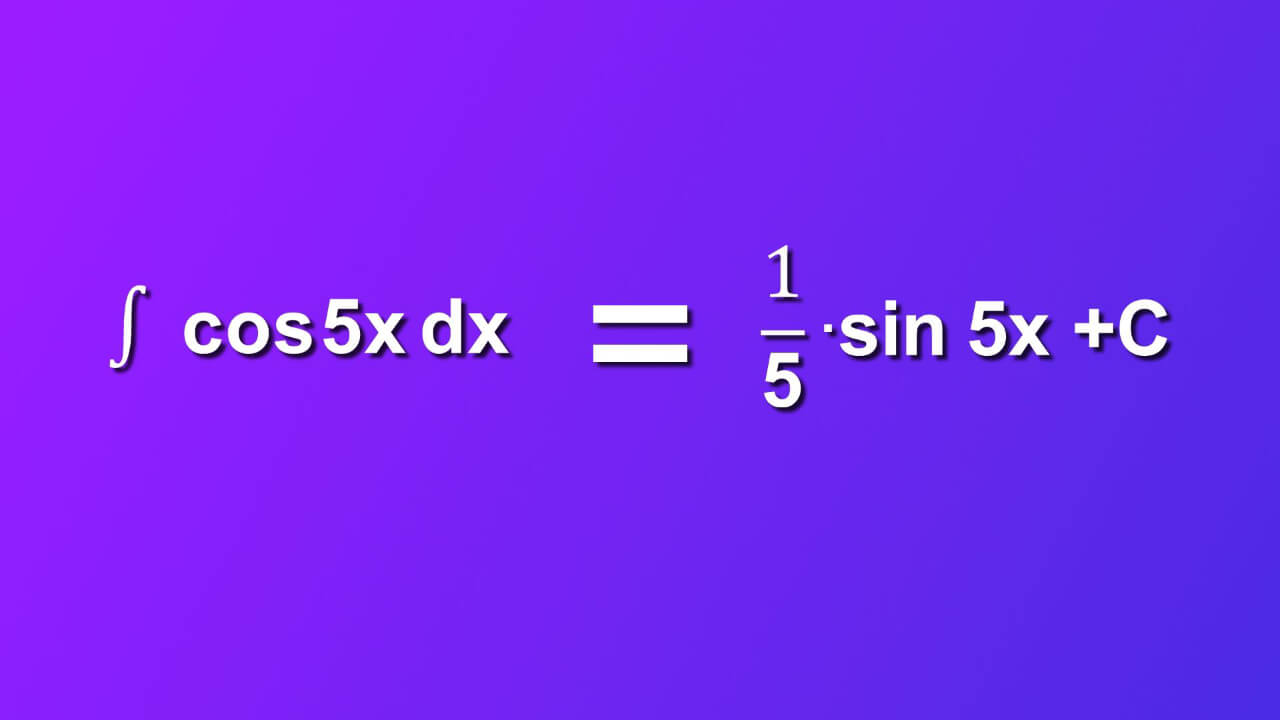
Dictionary
Integration (antidifferentiation)
Computation (process of finding) of an integral, opposite process to differentiation.Integrand
Function placed between sign of integral and differential of variable of integration e.g. $${{ \int f(x)dx}}$$,where:
$${{ \int }}$$- integration operator,
f(x) – integrand,
dx- differential of variable of integration x
Integrable function
Function that integral over its domain is finite.Indefinite integral
Represents a class of primitive functions whose derivative is the integrand e.g. $${{\int f(x)dx=F(x)+C \Leftrightarrow F’(x)=f(x)}}$$$${{C=const. }}$$,
$${{f, F,C \in R }}$$
R-real numbers
$${{\int f(x)dx}}$$ - indefinite integral of function f(x) by dx,
$${{F(x)+C}}$$ – a class of primitive functions that $${{F’(x)=f(x) }}$$,
F(x) - primitive function, usually written in capital letters,
R-real numbers.
Integration by substitution, substitution method, u-substitution
Method used to solve integral when an integral contains some function and its derivative. The function we sat as equal to u and we rewrite the integral using a new variable u.$${{\varphi: x \rightarrow \varphi (x)=u, x \in X, u \in U}}$$
and
$${{f: u \rightarrow f(u), u \in U, f(u) \in \varphi }}$$
$${{\varphi}}$$ is injective and differentiable function in X
f is continuous in U
then, $${{ \int f(\varphi (x)) \varphi’(x)dx=f(u) du}}$$ $${{\int f(\varphi (x))\varphi’(x)dx=\Bigg|\matrix{u= \varphi (x) \cr d(u)= d(\varphi (x))\cr du= \varphi ’(x) dx}\Bigg| =\int f(u) du}}$$
Function
Function specified on a set X and having values in set Y is an assignment each element of set X specifically one element in set Y.$${{f: X \rightarrow Y}}$$
f-function name,
X-set of elements of function f, domain of a function f
Y-set of function values of function f, codomain of a function f
$${{x\in X, y \in Y}}$$
$${{y=f(x) f: x\rightarrow y}}$$
$${{y=y(x), }}$$
y(x)-vales of the function named y,
x-independent variable,
y-dependent variable.
Derivative, derivative of a function
If $${{lim {\Delta f \over \Delta x }}}$$exists (and is finite), then this limit is named$${{ \Delta x\rightarrow 0}}$$
derivative of a function f(x) in a point x0 and use symbol f’(x).
$${{ f’(x_0) {\buildrel\rm def\over=} \lim_{\Delta x\to0} {\Delta f \over \Delta x}}}$$
Derivative function f’(x)
Derivative function of function f(x) is a function that values in a point x_0 are equal to derivative of this function in the point x_0.f’(x_0) - derivative of a function f(x) in a point x_0 (a number, because it is a specifically determined limit of a function),
f’(x)-derivative function.
Differentiable function
f(x) is differentiable in a point x_0 means that there exists f’(x_0 )-f(x) is differentiable in (a,b) means there exists f’(x), x $${{\in(a,b) }}$$
-f(x) is differentiable in



