How to solve indefinite integral of sine x divided by 4 minus cosine x by dx ?
Short answer: indefinite integral of sine x divided by 4 minus cosine x by dx is ln|4-cosx|+C. ∫ ((sin x)/(4 - cos x))dx is not particulary hard integral. You can solve it in 7 easy steps. We will walk you through and explain everything. Let's start.
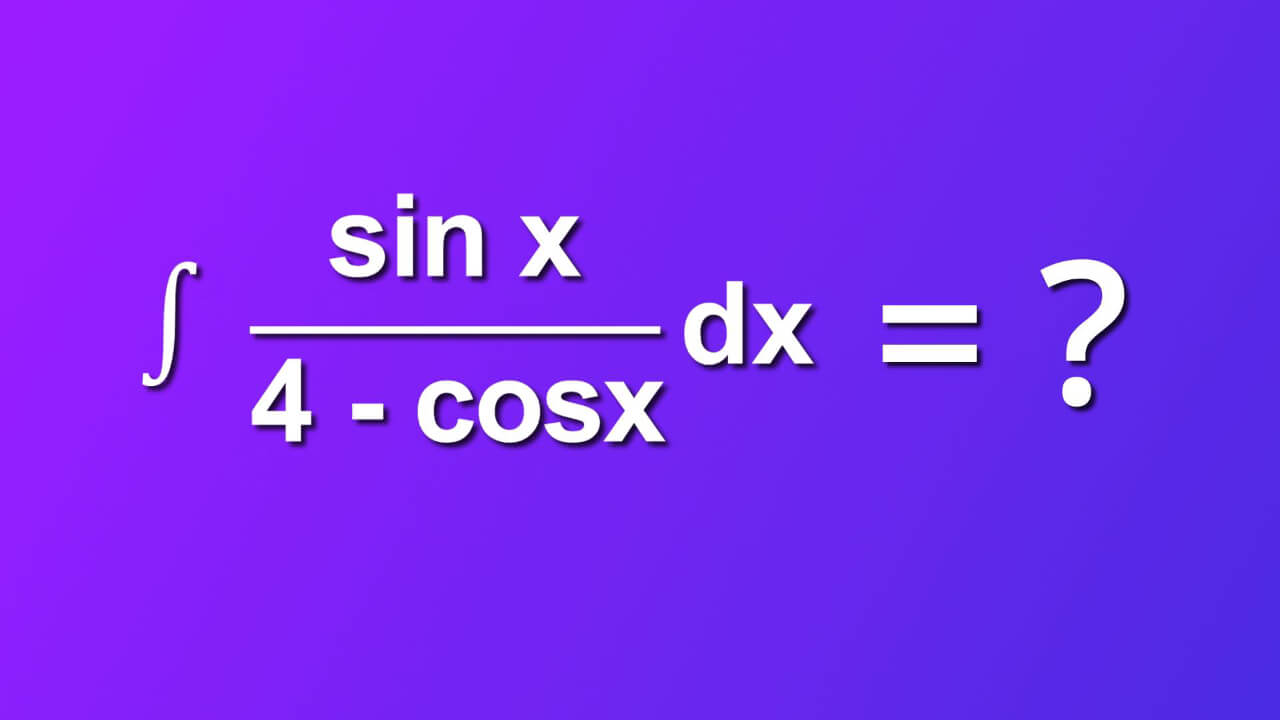
Table of contents
- Required assumtions
- Step by step solution of ∫ ((sin x)/(4 - cos x))dx
- What is indefinite integral of sine x divided by 4 minus cosine x by dx?
- Full video how to solve ∫ ((sin x)/(4 - cos x))dx
- Dictionary
- Want to solve next one?
Required assumtions
Usually, we have some additional info about function f of (x). In our case:
- f(x) belongs to real numbers
- f(x) is integrable in that domain
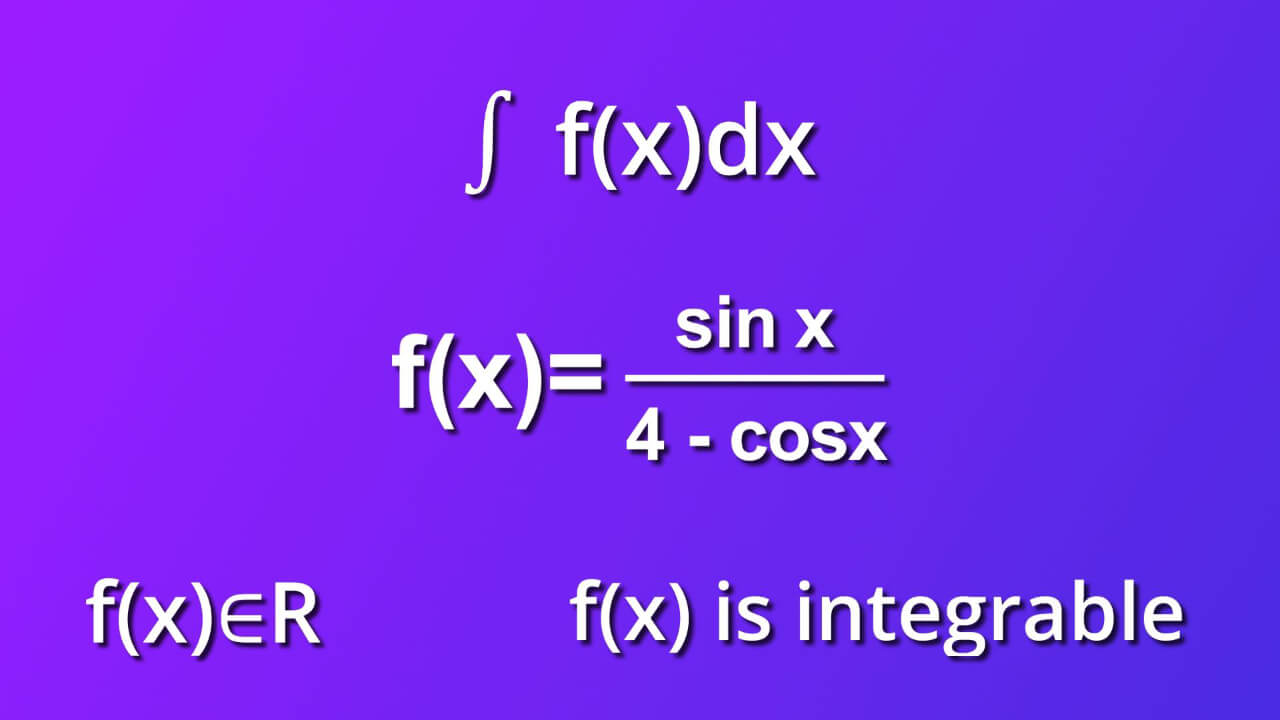
Step by step solution of ∫ ((sin x)/(4 - cos x))dx
We will solve ∫ ((sin x)/(4 - cos x))dx in 7 easy steps. Let's get started
Step 1
From symbol dx we know that differential of variable x indicates that the variable of integration is x. In that case, to solve this integral we may apply so called u−substitution method. We do it in order to modify the integral in the way that enable using some of formulas for finding integrals. Now, we try to substitute expression 4 minus cosine x.

Step 2
We say u is equal 4 minus cosine x. We also have to know what the derivative of u is. So we write derivative of u equals d (4 minus cosine x). So we’ve got du is equal to derivative of 4 minus cosine x multiplied by dx. From rules that we can apply to derivatives, we know that derivative of 4 minus cosine x equals derivative of 4 minus derivative of cosine x and the whole expression is multiplied by dx. Thus, we have du equals and first from derivative of 4 we get 0 as derivative of constant is zero. Then we have minus and derivative of cosine s equals minus sine s. In our case s is x and we’ ve got minus sine x multiplied by dx. Let’s rewrite it and get rid of two minuses before our sine x. We’ve got in result du is equal to sine x multiplied by dx. We can leave the expression like this as in a moment we insert it in exactly that form to our main equation.

Step 3
Let’s make use of our u. We insert u instead of 4 minus cosine x to our main equation and instead of the whole numerator multiplied by dx we can now insert du. Thus, we have integral of du divided by u in our main equation.

Step 4
We can rewrite this expression as integral of one divided by u multiplied by du. Perfect, now we can apply formula for solving integral of one divided by s by ds which equals natural logarithm of absolute value of s. We also must add constant C to make sure that we have all our solution taken into account as our solution make whole class of function not a single one. In our case s is equal to u.

Step 5
Then, we’ve got natural logarithm of absolute value of u plus constant C.

Step 6
But it is not the end of our solution. We must come back to our problem, and it was formulated using variable x. We used u-substitution and now we must come back to x. So instead of u we now insert 4 minus cosine x.
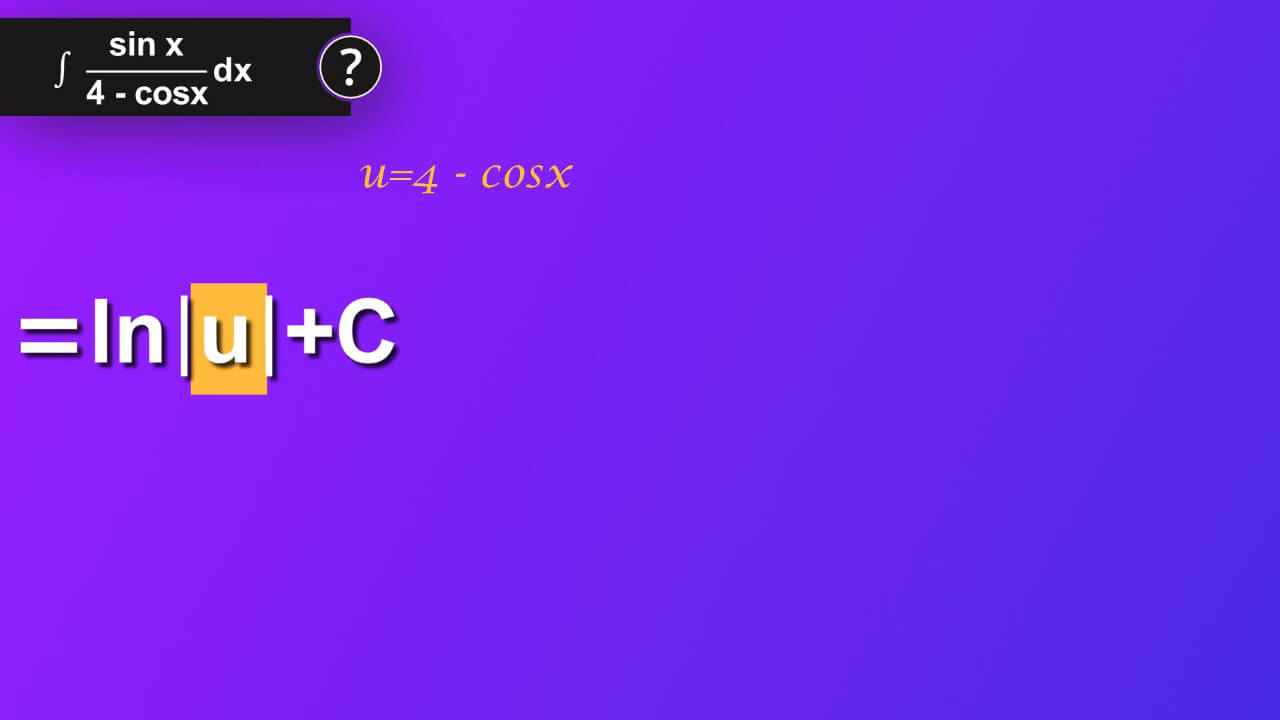
Step 7
We’ve got natural logarithm of absolute value of (4 minus cosine x) plus constant C as a result of our problem.
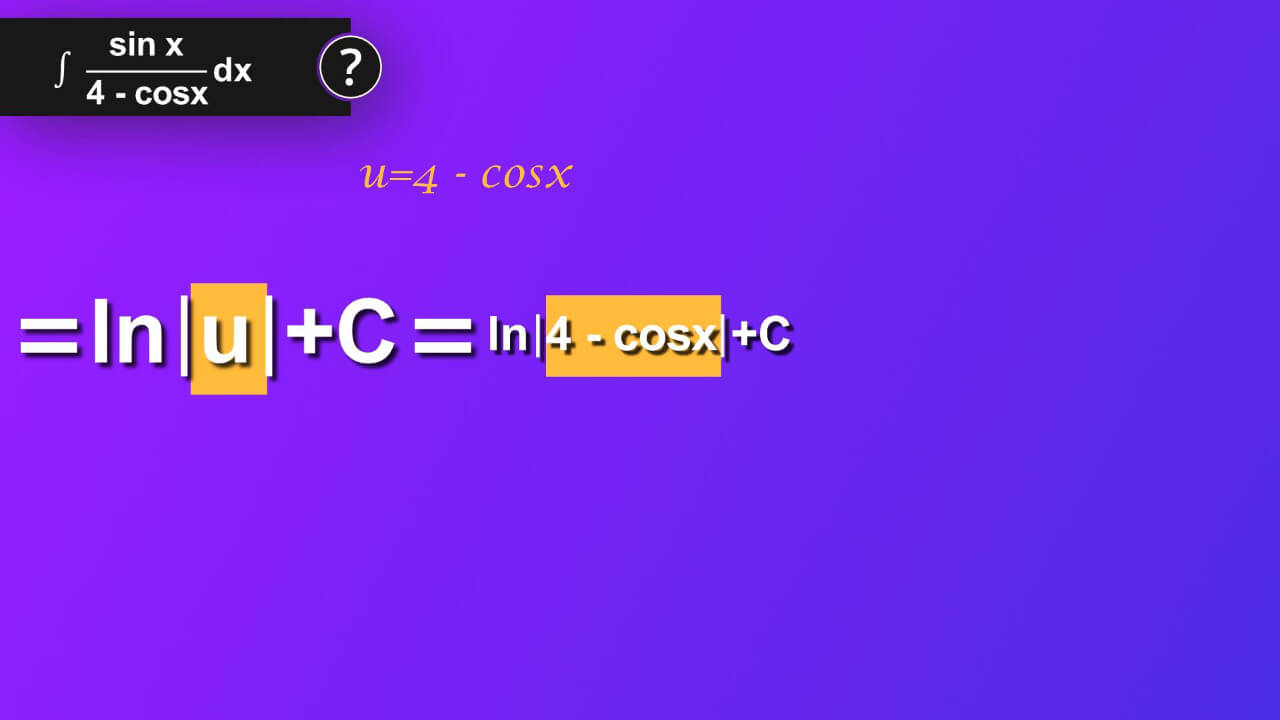
What is indefinite integral of sine x divided by 4 minus cosine x by dx?
We finally did it: ∫ ((sin x)/(4 - cos x))dx=ln|4-cosx|+C
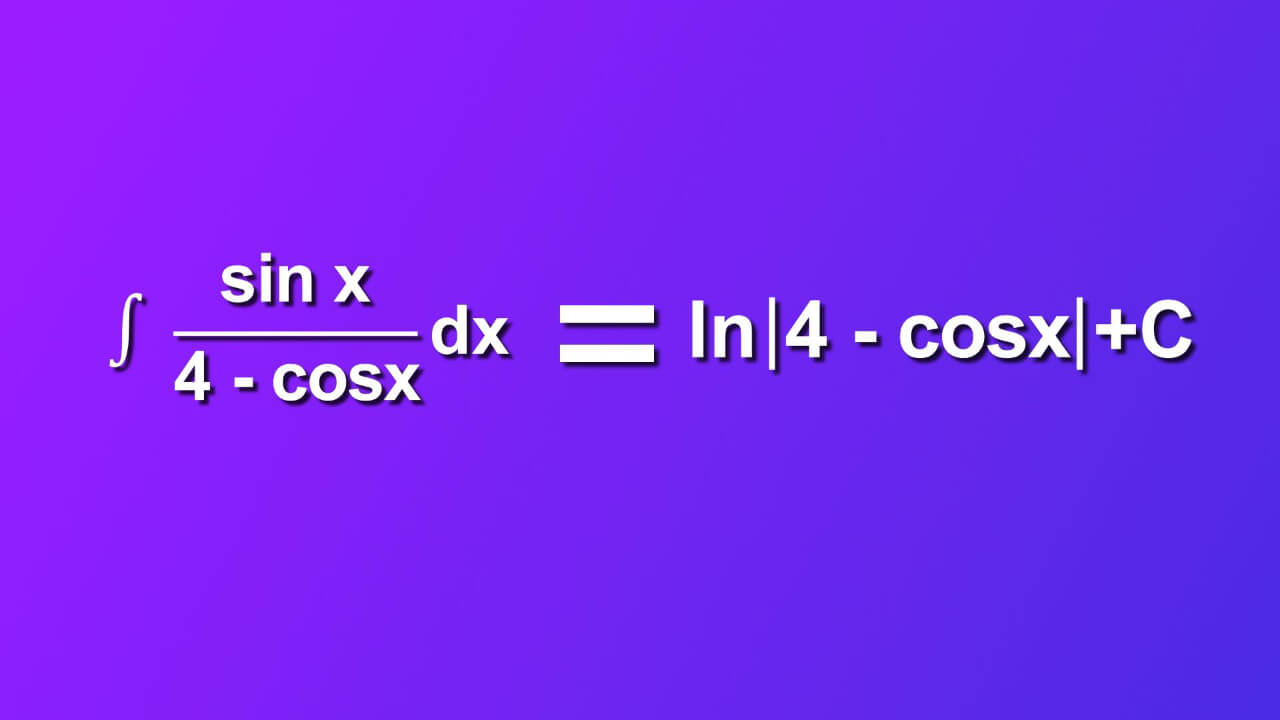
Dictionary
Integration (antidifferentiation)
Computation (process of finding) of an integral, opposite process to differentiation.Integrand
Function placed between sign of integral and differential of variable of integration e.g. $${{ \int f(x)dx}}$$,where:
$${{ \int }}$$- integration operator,
f(x) – integrand,
dx- differential of variable of integration x
Integrable function
Function that integral over its domain is finite.Indefinite integral
Represents a class of primitive functions whose derivative is the integrand e.g. $${{\int f(x)dx=F(x)+C \Leftrightarrow F’(x)=f(x)}}$$$${{C=const. }}$$,
$${{f, F,C \in R }}$$
R-real numbers
$${{\int f(x)dx}}$$ - indefinite integral of function f(x) by dx,
$${{F(x)+C}}$$ – a class of primitive functions that $${{F’(x)=f(x) }}$$,
F(x) - primitive function, usually written in capital letters,
R-real numbers.
Integration by substitution, substitution method, u-substitution
Method used to solve integral when an integral contains some function and its derivative. The function we sat as equal to u and we rewrite the integral using a new variable u.$${{\varphi: x \rightarrow \varphi (x)=u, x \in X, u \in U}}$$
and
$${{f: u \rightarrow f(u), u \in U, f(u) \in \varphi }}$$
$${{\varphi}}$$ is injective and differentiable function in X
f is continuous in U
then, $${{ \int f(\varphi (x)) \varphi’(x)dx=f(u) du}}$$ $${{\int f(\varphi (x))\varphi’(x)dx=\Bigg|\matrix{u= \varphi (x) \cr d(u)= d(\varphi (x))\cr du= \varphi ’(x) dx}\Bigg| =\int f(u) du}}$$
Function
Function specified on a set X and having values in set Y is an assignment each element of set X specifically one element in set Y.$${{f: X \rightarrow Y}}$$
f-function name,
X-set of elements of function f, domain of a function f
Y-set of function values of function f, codomain of a function f
$${{x\in X, y \in Y}}$$
$${{y=f(x) f: x\rightarrow y}}$$
$${{y=y(x), }}$$
y(x)-vales of the function named y,
x-independent variable,
y-dependent variable.
Composition of functions
Function f(x) and g(x) are specified on set X,$${{h: X\rightarrow T}}$$ and h(x)=t for x\inX and t\inT
$${{g: T\rightarrow Y}}$$
$${{x\in X, t\inT, y\in Y}}$$
$${{x \buildrel h\over\longrightarrow h(x) \buildrel g\over\longrightarrow g(t)=y}}$$
$${{x\rightarrow y=g(t)|_{t=h(x)}=g(h(x)) }}$$
$${{g(h(x)) }}$$ is a composition of two functions $${{ (g \circ h) (x) }}$$
$${{x \buildrel { g \circ h }\over\longrightarrow y=(g \circ h) (x) }}$$
where:
h-internal function,
g-external function.
Derivative, derivative of a function
If $${{lim {\Delta f \over \Delta x }}}$$exists (and is finite), then this limit is named$${{ \Delta x\rightarrow 0}}$$
derivative of a function f(x) in a point x0 and use symbol f’(x).
$${{ f’(x_0) {\buildrel\rm def\over=} \lim_{\Delta x\to0} {\Delta f \over \Delta x}}}$$
Derivative function f’(x)
Derivative function of function f(x) is a function that values in a point x_0 are equal to derivative of this function in the point x_0.f’(x_0) - derivative of a function f(x) in a point x_0 (a number, because it is a specifically determined limit of a function),
f’(x)-derivative function.
Differentiable function
f(x) is differentiable in a point x_0 means that there exists f’(x_0 )-f(x) is differentiable in (a,b) means there exists f’(x), x $${{\in(a,b) }}$$
-f(x) is differentiable in



