How to solve indefinite integral of x multiplied by square root of x divided by 5th root of x rise to the 4th power by dx ?
Short answer: indefinite integral of x multiplied by square root of x divided by 5th root of x rise to the 4th power by dx is (10/17)x(10th root of x^7)+C. ∫ (x sqrt root of x /(5th root of x^4) )dx is not particulary hard integral. You can solve it in 12 easy steps. We will walk you through and explain everything. Let's start.
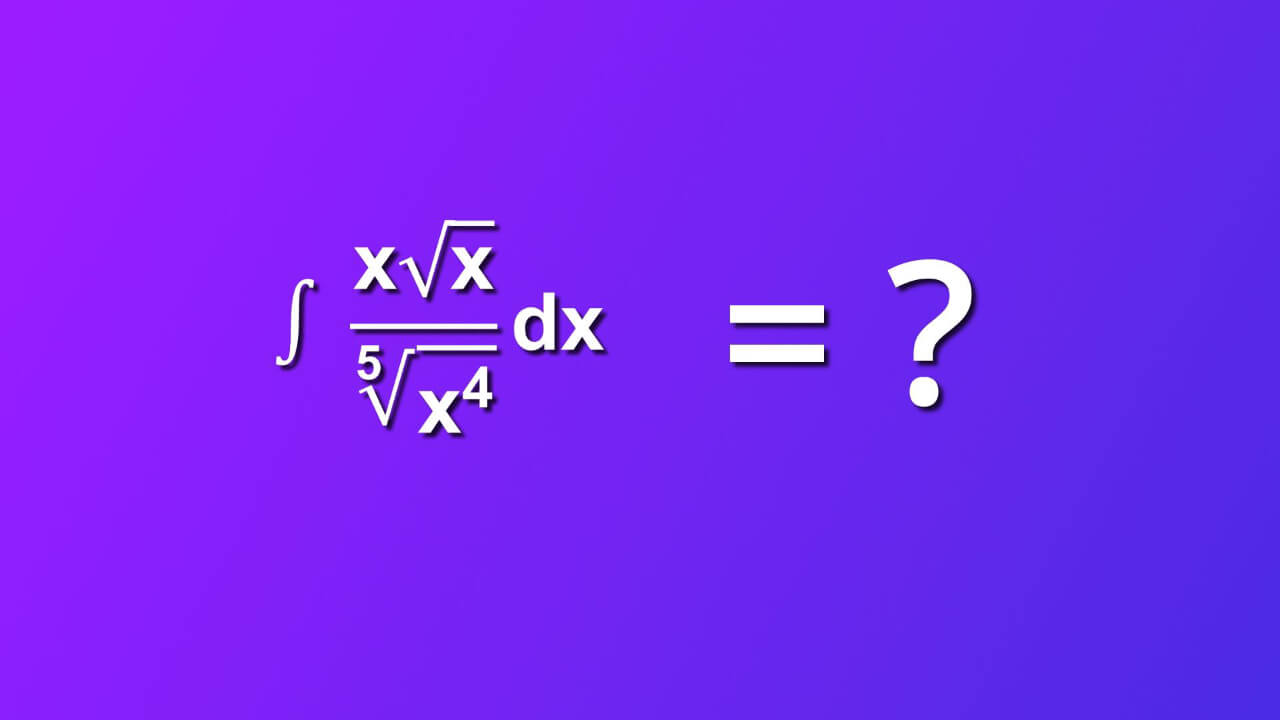
Table of contents
- Required assumtions
- Step by step solution of ∫ (x sqrt root of x /(5th root of x^4) )dx
- What is indefinite integral of x multiplied by square root of x divided by 5th root of x rise to the 4th power by dx?
- Full video how to solve ∫ (x sqrt root of x /(5th root of x^4) )dx
- Dictionary
- Want to solve next one?
Required assumtions
Usually, we have some additional info about function f of (x). In our case:
- f(x) belongs to real numbers
- f(x) is integrable in that domain

Step by step solution of ∫ (x sqrt root of x /(5th root of x^4) )dx
We will solve ∫ (x sqrt root of x /(5th root of x^4) )dx in 12 easy steps. Let's get started
Step 1
From symbol dx we know that differential of variable x indicates that the variable of integration is x. Let’s rewrite integrand - function inside the integral. We may apply formula which says n-th root of s equals s rise to one divided by n. First we can do it to numerator. In that case s is x and n is 2. And we have in numerator x multiplied by x rise to a half. The same formula we apply also for denominator. In that case s is x rise to 4, while n is 5.

Step 2
Thus we have in denominator x rise to 4th power and this rise to one-fifth. Now we may take advantage of the formula s rise to n and that rise to m equals s rise to n multiplied by m. In our case, if we want to apply it to denominator, s is x n is 4 and m is one-fifth.

Step 3
In that way we have x rise to four-fifth in denominator of our main solution.

Step 4
Let’s come back to the numerator. We can write s as s rise to power 1 and in our case, we will use this formula for our x in numerator and write it as x rise to 1. Then, knowing that s rise to n multiplied by s rise to m equals s rise to n plus m, we can rewrite our numerator. In our case s is x, n is 1 and m is a half.

Step 5
Thus we have x rise to one and a half and in denominator x rise to four-fifth. Now we can use formula s rise to n divided by s rise to m equals s rise to n minus m. In our case s equals x, n is one plus a half so we can write it as 2 seconds pluas a half and we have three seconds. While m is four-fifths -the power that we have in our denominator. And we may write our main solution as x rise to three-seconds minus four-fifths.
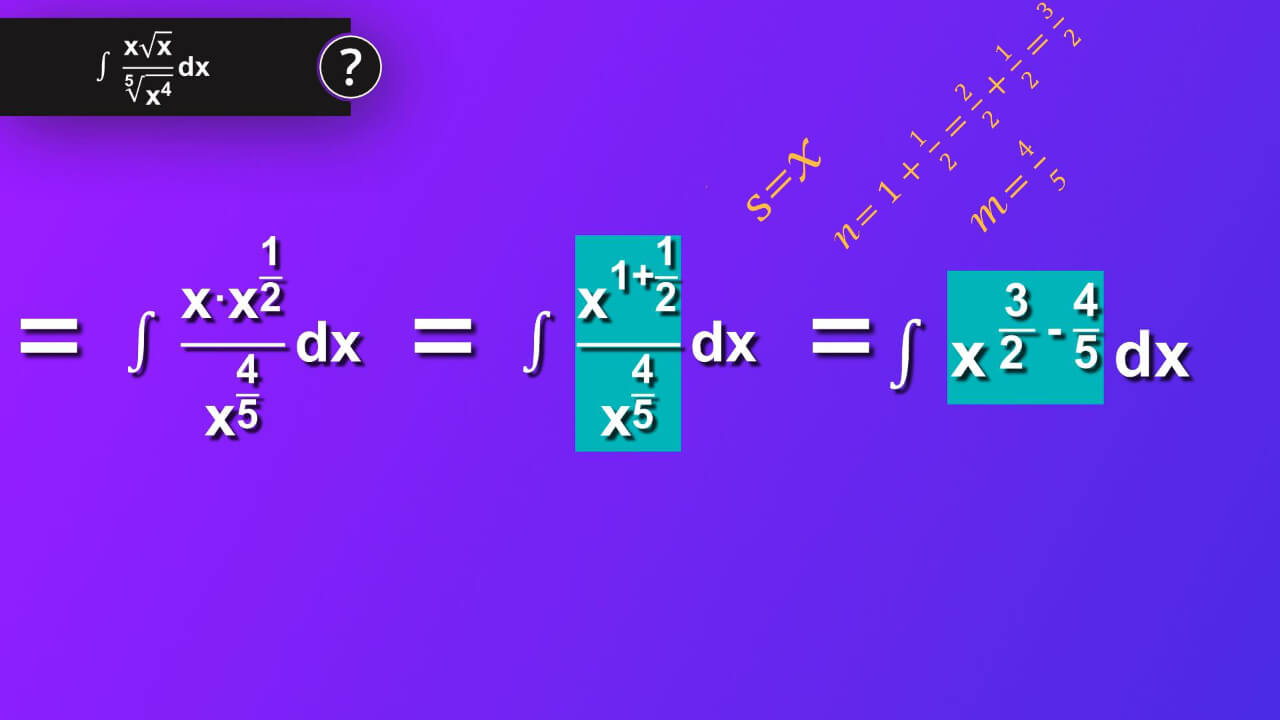
Step 6
We must subtract expression that we have in power. To do that we need common denominator and in our case we can just multiply denominator 2 by denominator 5 but we have to multiplied also numerator by the same number. In case of three-seconds we multiply it by one but expresse it as five- fifth and in that way we multiply numerator by 5 and denominator by 5. Then in case of four-fifths, we multiply it also by one but expressed as two-seconds and in that way we multiply numerator by 2 and denominator by 2 as well. We have now common denominator 10 and in numerator 15 minus 8, which give as a result seven -tenth. Then in our main equation, we have integrand of x rise to seven-tenth by dx.
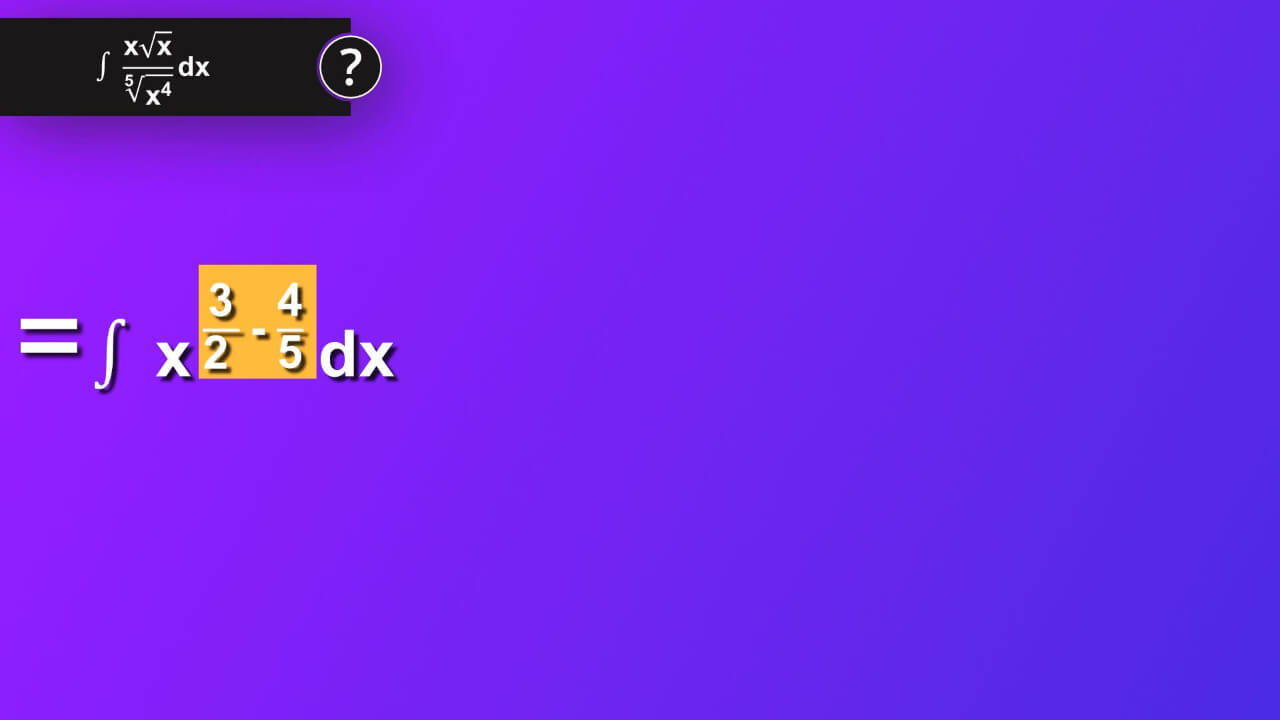
Step 7
And after all those modifications we can easily apply formula for solving integral of s rise to n which is s rise to n plus 1 divided by n+1. We also must add constant C to make sure that we have all our solution taken into account as our solution make whole class of function not a single one.
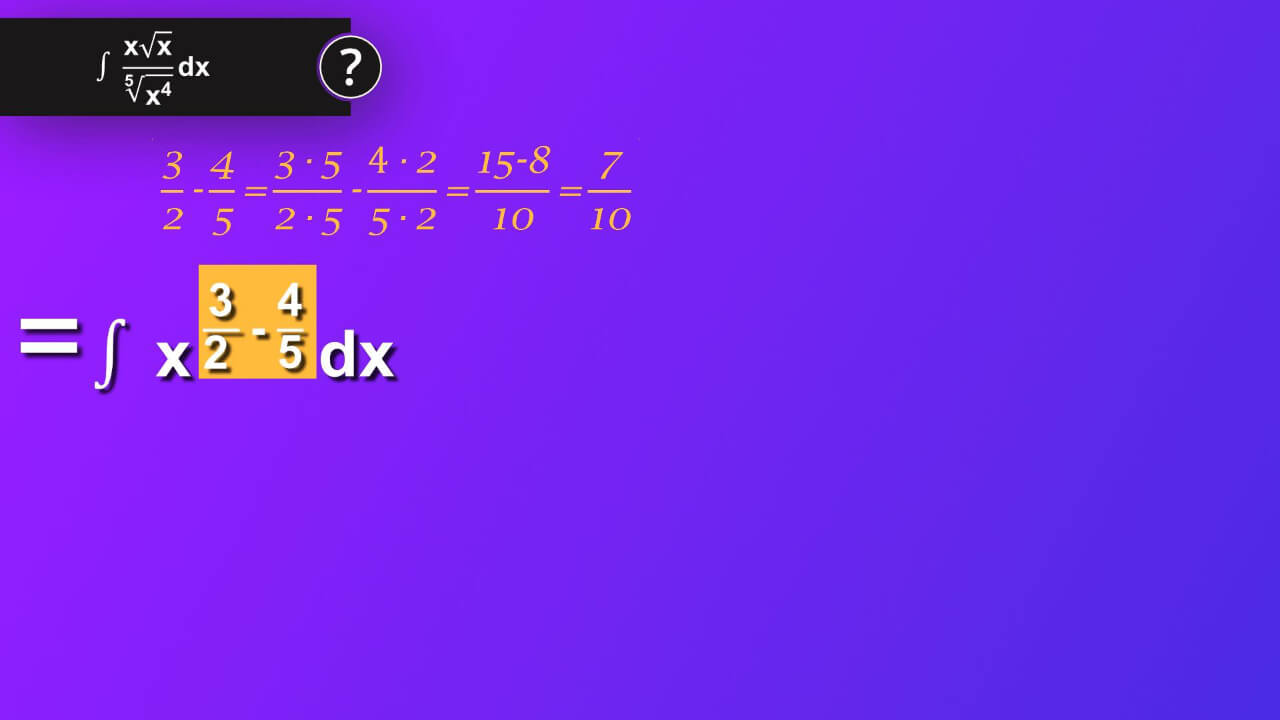
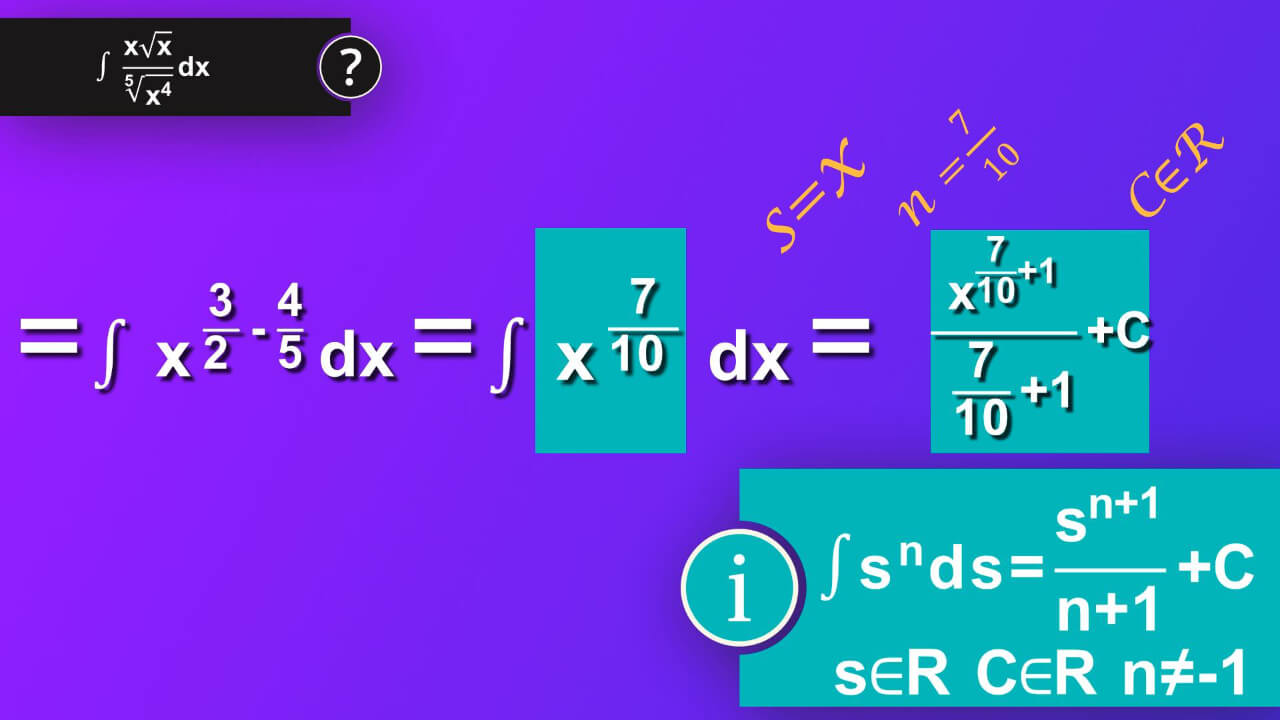
Step 8
And now in our case s is equal to x and n is seven-tenth. We’ve got x rise to seven-tenth plus 1 divided by is seven-tenth plus one and plus constant C.
Step 9
First, let’s just add 1 to seven tenth and we have seven tenth plus ten-tenth, thus we’ve got seventeen- tenth. We can write it down in numerator as x rise to seventeen-tenth and in denominator as just seventeen -tenth.

Step 10
We can smooth it a little taking advantage of formula which says that s divided by a divided by b equals b divided by a multiplied by s. In our case s is equal to x rise to seventeen-tenth, a is 17, b is 10. And we have ten-seventeenth multiplied by x rise to seventeen- tenth plus constant C.

Step 11
We may also express differently our x rise to seventeen-tenth and write the numerator power as 10 plus 7 and use formula which says that we can now treat it as two separate expressions x rise to ten-tenth and x rise to seven-tenth, multiplied by themselves. So we have x rise to 1 or just x and x rise to seven-tenth. Also x rise to 7divided by 10 we can rewrite knowing that s rise to n divided by m equals m-th root of s rise to n. In our case s is x, n is7, m is 10.

Step 12
As a result, we’ve got ten-seventeenth multiplied by tenth root of x rise to seven plus constant C.

What is indefinite integral of x multiplied by square root of x divided by 5th root of x rise to the 4th power by dx?
We finally did it: ∫ (x sqrt root of x /(5th root of x^4) )dx=(10/17)x(10th root of x^7)+C
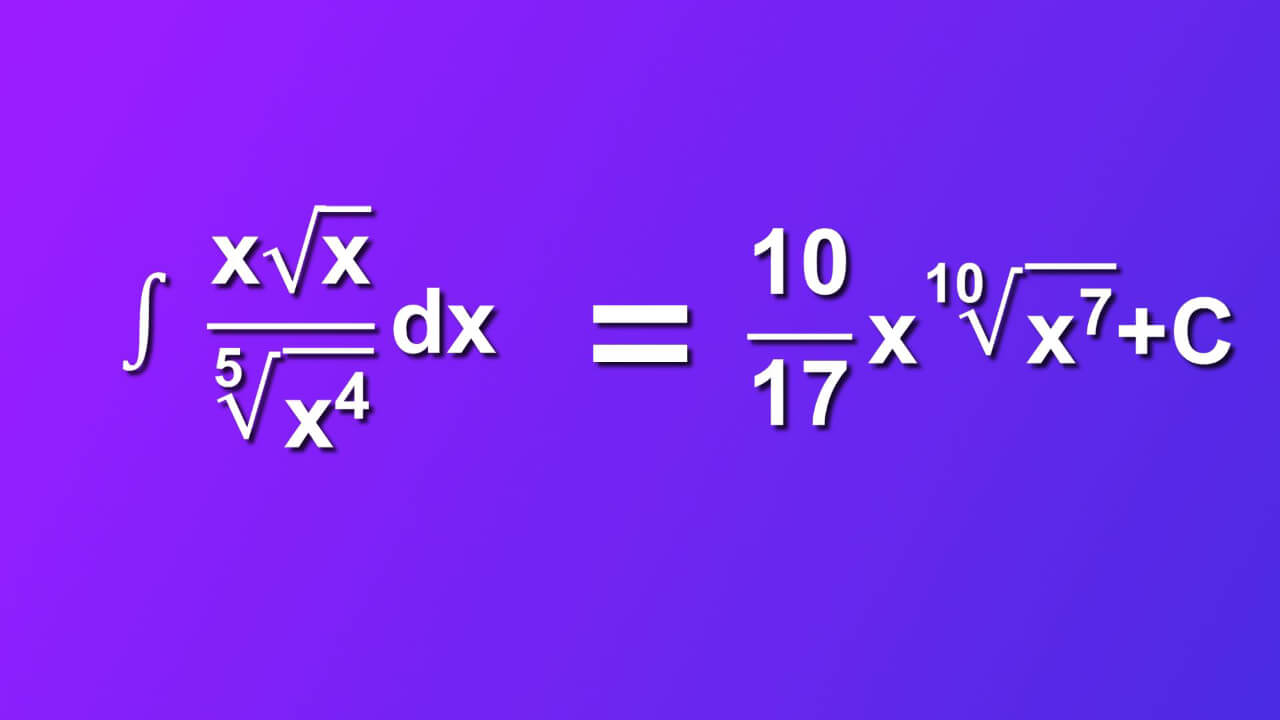
Dictionary
Integration (antidifferentiation)
Computation (process of finding) of an integral, opposite process to differentiation.Integrand
Function placed between sign of integral and differential of variable of integration e.g. $${{ \int f(x)dx}}$$,where:
$${{ \int }}$$- integration operator,
f(x) – integrand,
dx- differential of variable of integration x
Integrable function
Function that integral over its domain is finite.Indefinite integral
Represents a class of primitive functions whose derivative is the integrand e.g. $${{\int f(x)dx=F(x)+C \Leftrightarrow F’(x)=f(x)}}$$$${{C=const. }}$$,
$${{f, F,C \in R }}$$
R-real numbers
$${{\int f(x)dx}}$$ - indefinite integral of function f(x) by dx,
$${{F(x)+C}}$$ – a class of primitive functions that $${{F’(x)=f(x) }}$$,
F(x) - primitive function, usually written in capital letters,
R-real numbers.
Function
Function specified on a set X and having values in set Y is an assignment each element of set X specifically one element in set Y.$${{f: X \rightarrow Y}}$$
f-function name,
X-set of elements of function f, domain of a function f
Y-set of function values of function f, codomain of a function f
$${{x\in X, y \in Y}}$$
$${{y=f(x) f: x\rightarrow y}}$$
$${{y=y(x), }}$$
y(x)-vales of the function named y,
x-independent variable,
y-dependent variable.



